Libraries For Data Science - NumPy
By Adson Nogueira Alves
Introdução a Bibliotecas para Ciência de Dados - Parte 1 de 3
 Fonte: Reviewsreporter
Fonte: Reviewsreporter
Podemos dizer que Data Science ou Ciência de Dados é a combinação de métodos científicos, matemáticos e estatísticos que através de uma programação especializada e análises avançadas de Inteligência Artificial (IA) explora de forma profunda informações geralmente ignoradas de uma grande base de dados.
Um cientista de dados atua na preparação, análise e apresentação dos resultados, afim de revelar padrões e permitir tirar conclusões que ajudem de forma significativa nas tomadas de decisão de uma área de interesse. Essa preparação envolve ferramentas de manipulação e visualização de dados para identificar os padrões e tendências. Algoritmos e modelos de Inteligência Artificial poderam ser aplicados para ajudar nas predições.
O objetivo deste conteúdo é que você desenvolva suas primeiras habilidades como Cientista de Dados, atuando na preparação, análise e apresentação dos resultados. Para isso abordaremos bibliotecas essenciais ao tema.
Dessa forma, será feito uma introdução as bibliotecas:
💡 Incentivo fortemente que explore as documentações nos links acima.
Para o post não ficar muito extenso o conteúdo será dividido em 3 partes. Na primeira conversaremos sobre a biblioteca NumPy, na segunda falaremos sobre o Pandas e na terceira sobre o Matplotlib e o Seaborn.
Numpy
Segundo a documentação, NumPy é um pacote para computação científica em Python. Possuindo objetos array multidimensional e uma variedade de rotinas que possibilitam operações rápidas em matrizes, incluindo matemática, lógica, manipulação de formas, classificação, seleção, I/O, Transformações discreta de Fourier, álgebra linear básica, operações estatísticas básicas, simulação aleatória e muito mais.
A base do NumPy são objetos do tipo ndarray, que trabalham com dados multidimensionais. Algumas diferenças importantes entre o NumPy array e Python array padrão, são:
- O tamanho do ndarray tem um tamanho fixo na criação, alterar o seu tamanho significa apagar o original e criar um novo ndarray, evitando alocação de memoria desnecessária.
- Numpy facilita operações matemáticas além de outros tipos de operações para grande volume de dados.
- O Python array começa a se tornar ineficiente para tratar o crescente numero de dados matemáticos e científicos.
Mas porque usar Numpy ?
NumPy Arrays são mais rápidas e compactas do que as listas Python. Uma Array consome menos memória e é conveniente de usar. O NumPy usa muito menos memória para armazenar dados e fornece um mecânismo para especificar os tipos de dados. Isso permite que o código seja ainda mais otimizado.
Para começar a usar a biblioteca NumPy o único pré requisito é ter o Python instalado, caso ainda não tenha você pode obter orientações neste link.
o NumPy pode ser instalado utilizando o coda, o pip, um gerenciador de pacotes no macOS e Linux ou a partir da fonte.
- Caso utilize o Anaconda Distribution
conda install numpy- Caso utilize o pip
pip install numpyTestando no Ambiente de Programação
Você pode escolher qualquer interface de desenvolvimento (IDE) para testar as bibliotecas, porém sugiro que utilize o Colab, ou “Colaboratory”, que permite que você execute códigos em Python diretamente no seu navegador. Caso queira entender mais, neste link você tem um vídeo introdutório da ferramenta.
Para acessar as funções do NumPy é necessário importar a biblioteca para o código python. Onde np é apenas uma abreviação para melhor legibilidade do código.
import numpy as npNumPy Arrays
Uma Array é a estrutura de dados central da biblioteca NumPy. É uma grade de valores contendo informações sobre os dados brutos, indexação, localização e interpretação dos elementos.
Uma maneira de inicializar uma Array é a partir de listas Python, por exemplo
>> a = np.array([1, 2, 3, 4, 5, 6])Ou uma matriz de dimensão (3,4), como no exemplo abaixo:
>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])Para acessar os elementos da array usamos a indexação por colchetes começando em zero.
>> a = np.array([1, 2, 3, 4])
>> print(a)
[1 2 3 4]
>> print(a[2])
3Podemos nos referir a uma array de dimensão N como “ndarray”. Logo, um vetor representaria uma dimensão, uma matriz se refere a duas dimensões e para 3 dimensões ou mais o termo tensor é comumente usado. Em NumPy as dimensões são chamadas de eixos.
Como Criar um Array com NumPy
Para criar uma array com NumPy podemos utilizar a função np.array(). Para isso basta informar a lista de dados dentro da função, exemplo:
>> np.array([0,1,2,3])
[0 1 2 3]Ou ainda
>> np.array([[0,1,2,3],[4,5,6,7]])
[0 1 2 3]
[4 5 6 7]Podemos criar uma array totalmente preenchida com zeros, utilizando np.zeros(). Para isso informamos a dimensão e a quantidade desejada, exemplo:
>> np.zeros(4)
[0 0 0 0]Ou
>> np.zeros((4,4))
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]Ou uma array totalmente preenchida com uns 1, exemplo:
>> np.ones(3)
[1 1 1]Ou
>> np.ones((3,3))
[1 1 1]
[1 1 1]
[1 1 1]Podemos criar uma array com uma sequência determinada de elementos, exemplo:
>> np.arange(5)
array([0 1 2 3 4])Ou uma array com um intervalo uniformemente espaçado. Para isso, informamos o valor inicial, o valor final e o tamanho do passo. Exemplo:
>> np.arange(start=2, stop=9, step=2)
array([2, 4, 6, 8])Podemos utilizar também o np.linspace() para criar uma array com valores igualmente espaçados linearmente em um intervalo específico, exemplo:
>> np.linspace(0, 10, num=5)
array([ 0. , 2.5, 5. , 7.5, 10. ])Por padrão o tipo dos dados é um floating point (np.float64), porém podemos especificar o tipo de dado que queremos usando a keyword ‘dtype’. Exemplo:
>> x = np.ones(2, dtype=np.int64)
>> x
array([1, 1])Classificando elementos
Para isso vamos conhecer duas novas funções o np.sort() e o np.concatenate().
O np.sort() e uma forma simples de organizar os dados. Você pode especificar o eixo, o tipo e a ordem quando chamar a função. Um exemplo simples pode ser visto abaixo:
>> arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])
>> s = np.sort(arr)
>> s
array([1, 2, 3, 4, 5, 6, 7, 8])Leia mais sobre o sort() neste link.
O np.concatenate(), como o próprio nome sugere, tem o objetivo de concatenar o dado. Exemplo, se temos a e b:
>> a = np.array([1, 2, 3, 4])
>> b = np.array([5, 6, 7, 8])Aplicando o np.concatenate():
>> np.concatenate((a, b))
array([1, 2, 3, 4, 5, 6, 7, 8])Podemos ainda gerar uma variação de eixo, como:
>> x = np.array([[1, 2], [3, 4]])
>> y = np.array([[5, 6]])Onde teriamos:
>> np.concatenate((x, y), axis=0)
array([[1, 2],
[3, 4],
[5, 6]])Leia mais sobre o concatenate() neste link.
Formato e Tamanho de uma Array
Vamos conhecer ndarray.ndim, ndarray.size, ndarray.shape e arr.reshape().
Para isso vamos criar a seguinte Array:
>> arr = np.array([[[48, 80, 62],
[30, 47, 32],
[32, 49, 69]],
[[78, 44, 42],
[74, 72, 96],
[61, 55, 31]],
[[90, 69, 71],
[45, 69, 98],
[42, 82, 71]]])
Chegando na seguinte estrutura:
>> arr
array([[[48, 80, 62],
[30, 47, 32],
[32, 49, 69]],
[[78, 44, 42],
[74, 72, 96],
[61, 55, 31]],
[[90, 69, 71],
[45, 69, 98],
[42, 82, 71]]])Podemos descobrir o número de dimensões | eixos, executando:
>> arr.ndim
3
Observe, temos 3 dimensões ou 3 eixos.
Para encontrar o formato da array, executamos:
>> arr.shape
(3,3,3)ou seja, 3 elementos em cada uma das dimensões.
Para descobrir o tamanho da array, executamos:
>> arr.size
27Chegando em 27 elementos.
Podemos ainda alterar o formato de uma array sem alterar o dado, mantendo o mesmo numero de elementos da array original. Vamos utilizar o reshape() no arr criado anteriormente para isso.
O arr original:
>> arr
array([[[48, 80, 62],
[30, 47, 32],
[32, 49, 69]],
[[78, 44, 42],
[74, 72, 96],
[61, 55, 31]],
[[90, 69, 71],
[45, 69, 98],
[42, 82, 71]]])Nele temos o formato (3,3,3), visto abaixo.
>> arr.shape
(3,3,3)Alterando o nosso formato para uma configuração que respeite a quantidade de elementos poderiamos aplicar uma dimensão d1=3 e d2=9, para isso aplicamos o comando arr.reshape(3,9) mostrado abaixo:
>> arr.reshape(3,9)
array([[48, 80, 62, 30, 47, 32, 32, 49, 69],
[78, 44, 42, 74, 72, 96, 61, 55, 31],
[90, 69, 71, 45, 69, 98, 42, 82, 71]])Com np.reshape() poderiamos especificar alguns parâmetros opcionais, exemplo:
>> np.reshape(arr,newshape=(3,9),order='C')
array([[48, 80, 62, 30, 47, 32, 32, 49, 69],
[78, 44, 42, 74, 72, 96, 61, 55, 31],
[90, 69, 71, 45, 69, 98, 42, 82, 71]])Indexação e Fatiamento (slicing)
Podemos indexar e dividir arrays NumPy da mesma maneira que acontece em listas Python. Observe exemplo abaixo:
Array completa:
>> data = np.array([1, 2, 3])
>> data
array([1,2,3])Para mostrar o segundo elemento da array, usaríamos:
>> data[1]
2💡 Lembre que a posição de um elemento em uma array, assim como na lista em Python, sempre começa em zero.
Para mostrar todos os elementos até o segundo elemento, usaríamos.
>> data[:2]
array([1,2])Para mostrar todos os elementos a partir do segundo elemento, usaríamos.
>> data[1:]
array([2,3])Temos ainda a opção de trazer o último elementos, com:
>> data[-1]
3Ou ainda os últimos dois elementos, com:
>> data[-2:]
array([2, 3])A imagem abaixo apresenta um forma mais amigável de visualização de todos elementos citados acima.
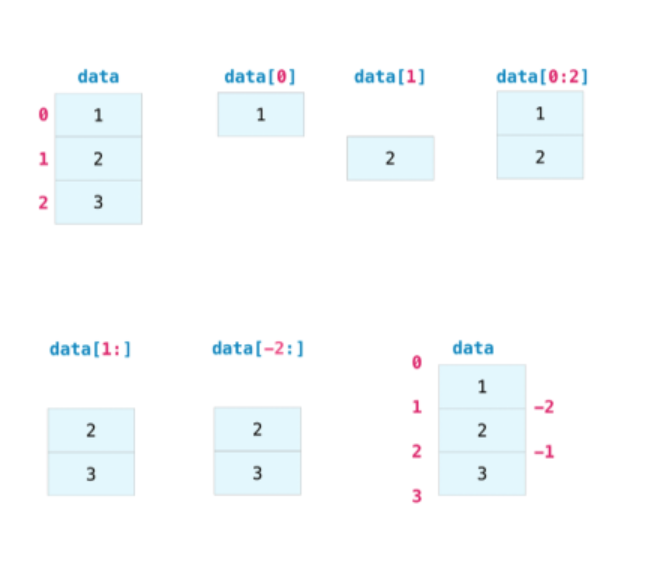 Fonte: Numpy Doc
Fonte: Numpy Doc
Para aprender mais sobre indexação e slicing acesse o link, porém falaremos mais na sequência.
Filtro
Uma operação de análise dos elementos de uma array pode ser gerada facilmente com NumPy. Para isso vamos usar a seguinte matriz:
>> arr = np.array([[1,2,3],[4,5,6],[7,8,9]])
>> arr
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])Logo, podemos verificar todos elementos pares com o seguinte comando:
>> arr[arr%2==0]
array([2, 4, 6, 8])Ou ainda todos valores maiores que 3
>> arr[arr>3]
array([4, 5, 6, 7, 8, 9])Ou uma união de ambos filtros
>> arr[(arr>3) & (arr%2==0)]
array([4, 6, 8])💡 Observe, na imagem abaixo, que temos um retorno booleano para cada um dos filtros utilizados anteriormente que especifica se o valor atende ou não a codicional, exemplo
>> arr > 5
array([[False, False, False],
[False, False, True],
[ True, True, True]])Podemos utilizar do np.nonzero() para retorno dos índices de alguma condicional (dim1, dim2, …), exemplo:
>> np.nonzero(arr%2==0)
(array([0, 1, 1, 2]), array([1, 0, 2, 1]))A primeira array da tupla representa os indices da primeira dimensão e o segundo array representa os indices da segunda dimensão.
Comprovação:
>> arr[np.nonzero(arr%2==0)]
array([2, 4, 6, 8])Criando uma Array a partir de dados existentes
Vamos estudar nessa seção funções que auxiliam nesta criação. Abordaremos procedimentos como o slicing e indexação , np.vstack(), np.hstack(), np.hsplit(), .view() e copy().
Vamos trabalhar com a seguinte array:
>> a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
>> a
array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])Para fazer um fatiamento (slicing) desse dados utilizamos o símbolo de ’:’ para determinar o inicio e o fim da seleção, observe:
>> arr1 = a[3:8]
>> arr1
array([4, 5, 6, 7, 8])Podemos empilhar existentes arrays a partir do vstack e hstack. Vamos considerar as matrizes abaixo.
>> a1 = np.array([[1, 1],
... [2, 2]])
>> a2 = np.array([[3, 3],
... [4, 4]])Para empilhar verticalmente usamos o vstack, exemplo:
>> np.vstack((a1, a2))
array([[1, 1],
[2, 2],
[3, 3],
[4, 4]])Para empilhar horizontalmente usamos o hstack, exemplo:
>> np.hstack((a1, a2))
array([[1, 1, 3, 3],
[2, 2, 4, 4]])Outra função interesante é o np.hsplit(), com ela é possível “fatiar” uma array em sub-arrays de igual tamanho. Exemplo:
>> x = np.arange(16.0).reshape(4, 4)
>> x
array([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]])
>> np.hsplit(x, 2)
[array([[ 0., 1.],
[ 4., 5.],
[ 8., 9.],
[12., 13.]]),
array([[ 2., 3.],
[ 6., 7.],
[10., 11.],
[14., 15.]])]💡 Aprenda mais sobre stacking e splitting aqui.
Ainda em criação de arrays, você pode usar o método view() para criar um novo objeto array que visualiza os mesmos dados que a array original.
As visualizações são um conceito importante do NumPy!
As funções NumPy, bem como operações como indexação e slicing, retornarão visualizações sempre que possível. Isso economiza memória e é mais rápido (nenhuma cópia dos dados precisa ser feita). No entanto, é importante estar ciente que
Modificar dados em uma visualização também modifica a matriz original!
Usando a array a abaixo como exemplo
>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])Observe atentamente o que acontece quando executando cada etapa abaixo
>> b1 = a[0, :]
>> b1
array([1, 2, 3, 4])
>> b1[0] = 99
>> b1
array([99, 2, 3, 4])
>> a
array([[99, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])Observe que quando modificamos um elemento de uma array filha (b1), a mesmo modificação acontece na array pai (a). Para que isso seja evitado podemos utilizar a função copy(), alterando apenas o primeiro trecho do código acima. Ficaria assim
>> b1 = a[0, :].copy()Operações Básicas
Operações de soma, subtração, multiplicação e divisão são facilmente implementadas com NumPy. Arrays de um mesmo shape podem ser executados diretamente com o sinal da operação (+, -, *, /). Exemplo:
>> np.array([1,2,3,4,5]) + np.array([2,2,2,2,2])
array([3, 4, 5, 6, 7])
>> np.array([1,2,3,4,5]) - np.array([2,2,2,2,2])
array([-1, 0, 1, 2, 3])
>> np.array([1,2,3,4,5]) * np.array([2,2,2,2,2])
array([ 2, 4, 6, 8, 10])
>> np.array([1,2,3,4,5]) / np.array([2,2,2,2,2])
array([0.5, 1. , 1.5, 2. , 2.5])Para somar os elementos de uma array uma opção é utilizar o sum(), exemplo:
>> a = np.array([1, 2, 3, 4])
>> a.sum()
10Caso esteja traballhando com uma array com mais de uma dimensão, podemos determinar qual eixo queremos fazer a operação através do argumento axis, basta atribuir de [0 … n] de acordo com o formato da array. Exemplo:
>> b = np.array([[1, 1], [2, 2]])
>> b.sum(axis=0)
array([3, 3])
>> b.sum(axis=1)
array([2, 4])Broadcasting
Broadcasting é um mecânismo que permite que o NumPy execute operações em matrizes de diferentes formas. A dimensão das matrizes devem ser compatíveis, por exemplo, quando as dimensões de ambas as matrizes são iguais ou quando uma delas é 1. Se as dimensões não forem compatíveis, você receberá um ValueError. Um exemplo simples pode ser visto abaixo.
>> data = np.array([1.0, 2.0])
>> data * 1.6
array([1.6, 3.2])Outras operações úteis com NumPy
Consederemos a matriz a sendo:
>> a = np.array([[0.45053314, 0.17296777, 0.34376245, 0.5510652],
[0.54627315, 0.05093587, 0.40067661, 0.55645993],
[0.12697628, 0.82485143, 0.26590556, 0.56917101]])
>> a
array([[0.45053314, 0.17296777, 0.34376245, 0.5510652],
[0.54627315, 0.05093587, 0.40067661, 0.55645993],
[0.12697628, 0.82485143, 0.26590556, 0.56917101]])Poderiamos facilmente encontrar valores de minimo, máximo e média com as funções .min(), .max(), .mean() veja:
>> a.max()
0.82485143
>> a.min()
0.05093587
>> a.mean()
0.40496486Valores Pseudo-aleatórios
Através do random.Generator é possível gerar números pseudo-aleatórios. Tudo o que você precisa fazer é passar a quantidade de elementos que deseja gerar:
>> rng = np.random.default_rng()
>> rng.random(3)
array([0.63696169, 0.26978671, 0.04097352])Observe que foram gerados valores entre [0,1]. Você poderia utilizar o random.uniform() para gerar valores float em um determinado intervalo:
>> np.random.uniform(low=1,high=90,size=(2,2))
array([[13.48994415, 44.5893233 ],
[77.76080021, 18.00994178]])O random.randint() ou ainda o rng.integers() geram valores int em um determinado intervalo:
>> np.random.randint(low=1,high=90,size=(2,2))
array([[43, 50],
[55, 88]])
>> rgn.integers(low=1,high=90,size=(2,2))
array([[84, 89],
[26, 47]])Retorno e Contagem de elementos únicos
Uma ação bem frequente é a verificação e a contagem de elementos únicos em uma array. Podemos obter essas informações facilmente com as função np.unique(). Veja o exemplo:
>> a = np.array([11, 11, 12, 13, 13, 15, 13, 17, 12, 13, 11, 14, 11, 19, 13])
>> a
array([11, 11, 12, 13, 13, 15, 13, 17, 12, 13, 11, 14, 11, 19, 13])
>> np.unique(a)
array([11, 12, 13, 14, 15, 17, 19])
>> np.unique(a, return_counts=True)
(array([11, 12, 13, 14, 15, 17, 19]),
array([4, 2, 5, 1, 1, 1, 1]))Podemos ainda saber os índices das primeira ocorrências de cada elemento único, veja exemplo:
>> np.unique(a, return_index=True)
(array([11, 12, 13, 14, 15, 17, 19]),
array([ 0, 2, 3, 11, 5, 7, 13]))💡 Na tupla a primeira array representa os elementos únicos e a segunda a contagem ou o indice, dependendo do argumento escolhido.
Funções de manipulação
Outras funções de manipulação bem úteis são a transposição, a inversão e o flatten (“esticamento”) dos elementos.
Para isso, vamos falar sobre o ndarray.transpose(), ndarray.T, np.flip(), ndarray.flatten() e o ndarray.ravel().
Veja os exemplos:
>> x = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
>> x.transpose()
array([[ 1, 5, 9],
[ 2, 6, 10],
[ 3, 7, 11],
[ 4, 8, 12]])
>> x.T
array([[ 1, 5, 9],
[ 2, 6, 10],
[ 3, 7, 11],
[ 4, 8, 12]])
>> np.flip(x)
array([[12, 11, 10, 9],
[ 8, 7, 6, 5],
[ 4, 3, 2, 1]])
>> x.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
>> x.ravel()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])💡 O ndarray.transpose() e ndarray.T são idênticos, logo a escolha de um ou de outro é indiferente.
Já o ndarray.flatten() e o ndarray.ravel() apesar de apresentarem um mesmo resultado, eles atuam de formas diferentes no dado. Enquanto o ndarray.flatten() cria uma nova variável o .ravel() não, dessa forma todo elemento alterado na variável gerada a partir do .ravel() afetará também a variável original. Semelhante ao que foi visto no view() anteriormente.
Salvar e carregar objetos NumPy
As últimas funções exploradas neste post serão as de salvamento e carregamento dos objetos NumPy.
Para isso vamos definir nossa variável a:
>> a = np.array([1, 2, 3, 4, 5, 6])
>> a
array([1, 2, 3, 4, 5, 6])Você pode salvar a em um arquivo “arquivo.npy” with:
>> np.save("arquivo",a)Para fazer a leitura de um “arquivo.npy” executamos:
>> b= np.load("arquivo.npy")
>> print(b)
[1 2 3 4 5 6]Além da opção de salvar o dado como .npy também é possivel salvar como .csv ou .txt. Para isso usamos a função .savetxt().
Exemplo:
>> a = np.array([1, 2, 3, 4, 5, 6])
>> np.savetxt("arquivo_csv.csv",a)Também é fácil fazer a leitura deste arquivo.
>> np.loadtxt('arquivo_csv.csv')
array([1., 2., 3., 4., 5., 6., 7., 8.])Parabéns por ter chegado ao final de mais um conteúdo, em breve sairá a Parte 2 de 3 do post, explorando a biblioteca Pandas.
Até lá =D.